dewipmeilinda

MATRIKS DETERMINAN (lanjutan) & INVERS

I. DETERMINAN

A.Matriks Ordo 3x3

Determinan matriks merupkan salah satu persyatan yang harus dipenuhi dalalm mencari invers suatu matriks. Dalam matriks, cara mencari determinan berbeda untuk setiap ordonya. Kali ini saya akan membahas mengenai cara menentukan determinan matriks ordo 3x3.

Untuk menentukan determinan matriks ordo 3x3 berbeda dengan cara menentukan determinan matriks ordo 2x2, untuk menentukannya yaitu pertama harus menambahkan kolom satu dan kolom dua secara berurutan ke sebelah kiri matriks. Untuk lebih jelasnya perhatikan uraian dibawah ini :

Keterangan :

DM : Determinan Matriks
Ordo : Jenis matriks
a, b, c, d, e, f, g, h, dan i : Elemen-elemen matriks

Contoh :
Tentukan determinan dari matriks di bawah ini !

Jawaban :

a. Metode Sarrus

Metode sarrus atau juga sering orang menyebutnya metode anyaman (Basketweave Method) adalah jalan alternatif dalam menghitung determinan dari matriks

3 \times 3

Perhatikan ilustrasi berikut :

Berdasarkan ilustrasi di atas kita peroleh langkah-langkah menghitung determinan matriks

3 \times 3

dengan metode sarrus sebagai berikut.

Tahapan Metode Sarrus dalam Mencari Determinan

Misalkan didefinisikan matriks

A_{3 \times 3}

sebagai berikut :

\begin{array}{ccc} _{} & _{} & _{} \\ _{} & _{} & _{} \\ _{} & _{} & _{} \end{array}

Langkah pertama dalam menentukan determinan dengan aturan sarrus yaitu dengan menambahkan secara berurutan kolom ke-

1

dan ke-

2

pada sebelah kanan kolom ke-

3

\begin{array}{ccccc} _{} & _{} & _{} & _{} & _{} \\ _{} & _{} & _{} & _{} & _{} \\ _{} & _{} & _{} & _{} & _{} \end{array}

Selanjutnya kita coret entri-entri pada diagonal utama dan diagonal lainnya.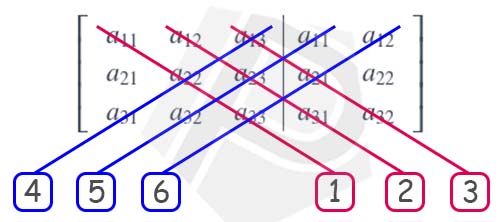 Tahapan Metode Sarrus

Sehingga diperoleh 6 bagian, kemudian kita kalikan entri-entri yang terletak pada kotak 1 sampai kotak 6.

_{}_{}_{}

_{}_{}_{}

_{}_{}_{}

_{}_{}_{}

_{}_{}_{}

_{}_{}_{}

Langkah terakhir yaitu menghitung determinan dengan mengurangkan jumlah hasil kali pada diagonal-diagonal utama(kotak 1, kotak 2 dan kotak 3) dengan jumlah hasil kali pada diagonal-diagonal pelengkapnya(kotak 4, kotak 5 dan kotak 6).

det (A) = 1 + 2 + 3 - 4 - 5 - 6 = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 - a 13 a 22 a 31 - a 11 a 23 a 32 - a 12 a 21 a 33

B. Metode Minor & Kofaktor

-Kofator

Setelah mendapatkan harga minor dari masing-masing elemen matriks kita dapat menentukan nilai atau harga dari kofaktor. Cara mencarinya adalah dengan mengalikan masing-masing nilai minor di atas dengan tanda tempat masing-masing elemen. Adapun tanda tempatnya dapat dilihat pada gambar berikut:

Jadi berdasarkan tanda tempat di atas kita dapat mencari nilai kofakto dari masing-masing elemen matriks. Untuk selanjutnya kita akan berikan simbol untuk nilai kofaktor masing-masing elemen dengan Cij, dimana i menandakan baris dan j menandakan kolom. jadi untuk setiap elemen di atas kita dapatkan harga kofaktornya sebagai berikut:

- Minor

Untuk mencari nilai kofaktor terlebih dahulu kita harus mencari nilai minor dari setiap elemen matrik. Untuk memudahkan, selanjutnya minor kita beri simbol dengan huruf M dan minor untuk setiap elemen matrik akan kita beri simbol dengan Mij dimana i adalah letak baris dan j adalah letak kolom dari setiap elemen matrik.

contoh:

diketahui matrik A sebagai berikut:

maka minor elemen 2 yang terletak pada baris ke 1 kolom ke 1 diberi simbol dengan M11. Untuk mencari harga minornya dapat kita lakukan dengan mencoret atau menghilangkan baris ke 1 dan kolom ke 1 sehingga didapatkan matrik baru seperti berikut:

minor elemen 2 (M11) adalah :

Serupa dengan cara di atas , minor elemen 3 (M12) adalah :

Untuk nilai M13, M21, M22, M23, M31, M32 dan M33 didapatkan hasil sebagai berikut:

C. Metode Ekspansi Laplace

Dalam aljabar linier , ekspansi Laplace , dinamai menurut Pierre-Simon Laplace , juga disebut ekspansi kofaktor , adalah ekspresi penentu | B | dari n × matriks B yang merupakan jumlah tertimbang dari penentu n sub-matriks (atau anak di bawah umur ) dari B , masing-masing ukuran ( n - 1) × ( n - 1). Perluasan Laplace adalah minat didaktik untuk kesederhanaannya dan sebagai salah satu dari beberapa cara untuk melihat dan menghitung determinan. Untuk matriks besar, dengan cepat menjadi tidak efisien jika dibandingkan dengan metode yang menggunakan dekomposisi matriks .

Kofaktor i , j dari matriks B adalah skalar C ij yang didefinisikan oleh

C_{ij}\ =(-1)^{i+j}M_{ij}\,,

C_ {ij} \ = (-1) ^ {i + j} M_ {ij} \ ,,

di mana M ij adalah i , j minor B , yaitu penentu ( n - 1) × ( n - 1) matriks yang dihasilkan dari menghapus baris ke- i dan kolom ke- j dari B.

Kemudian ekspansi Laplace diberikan sebagai berikut

Teorema . Misalkan B = [ b ij ] adalah matriks n × n dan perbaiki i , j ∈ {1, 2, ..., n }.

Kemudian determinannya | B | diberikan oleh:

{\begin{aligned}|B|&=b_{i1}C_{i1}+b_{i2}C_{i2}+\cdots +b_{in}C_{in}\\[5pt]&=b_{1j}C_{1j}+b_{2j}C_{2j}+\cdots +b_{nj}C_{nj}\\[5pt]&=\sum _{j'=1}^{n}b_{ij'}C_{ij'}=\sum _{i'=1}^{n}b_{i'j}C_{i'j}\end{aligned}}

{\ displaystyle {\ begin {aligned} | B | & = b_ {i1} C_ {i1} + b_ {i2} C_ {i2} + \ cdots + b_ {in} C_ {in} \\ [5pt] & = b_ {1j} C_ {1j} + b_ {2j} C_ {2j} + \ cdots + b_ {nj} C_ {nj} \\ [5pt] & = \ jumlah _ {j '= 1} ^ {n} b_ {ij '} C_ {ij'} = \ jumlah _ {i '= 1} ^ {n} b_ {i'j} C_ {i'j} \ end {aligned}}}

dimana

b_{in,in}

b_{jn,jn}

Pertimbangkan matriksnya

B={\begin{bmatrix}1&2&3\\4&5&6\\7&8&9\end{bmatrix}}.

B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}.

Penentu matriks ini dapat dihitung dengan menggunakan ekspansi Laplace di sepanjang salah satu baris atau kolomnya. Misalnya, ekspansi di sepanjang baris pertama menghasilkan:

{\begin{aligned}|B|&=1\cdot {\begin{vmatrix}5&6\\8&9\end{vmatrix}}-2\cdot {\begin{vmatrix}4&6\\7&9\end{vmatrix}}+3\cdot {\begin{vmatrix}4&5\\7&8\end{vmatrix}}\\[5pt]&=1\cdot (-3)-2\cdot (-6)+3\cdot (-3)=0.\end{aligned}}

{\begin{aligned}|B|&=1\cdot {\begin{vmatrix}5&6\\8&9\end{vmatrix}}-2\cdot {\begin{vmatrix}4&6\\7&9\end{vmatrix}}+3\cdot {\begin{vmatrix}4&5\\7&8\end{vmatrix}}\\[5pt]&=1\cdot (-3)-2\cdot (-6)+3\cdot (-3)=0.\end{aligned}}

Laplace expansion sepanjang kolom kedua menghasilkan hasil yang sama:

{\begin{aligned}|B|&=-2\cdot {\begin{vmatrix}4&6\\7&9\end{vmatrix}}+5\cdot {\begin{vmatrix}1&3\\7&9\end{vmatrix}}-8\cdot {\begin{vmatrix}1&3\\4&6\end{vmatrix}}\\[5pt]&=-2\cdot (-6)+5\cdot (-12)-8\cdot (-6)=0.\end{aligned}}

{\begin{aligned}|B|&=-2\cdot {\begin{vmatrix}4&6\\7&9\end{vmatrix}}+5\cdot {\begin{vmatrix}1&3\\7&9\end{vmatrix}}-8\cdot {\begin{vmatrix}1&3\\4&6\end{vmatrix}}\\[5pt]&=-2\cdot (-6)+5\cdot (-12)-8\cdot (-6)=0.\end{aligned}}

Mudah untuk memverifikasi bahwa hasilnya benar: matriks itu tunggal karena jumlah kolom pertama dan ketiga adalah dua kali kolom kedua, dan karenanya determinannya adalah nol.

Bukti

Laplace ekspansi determinan dengan anak di bawah umur yang saling melengkapi

Ekspansi kofaktor Laplaces dapat digeneralisasi sebagai berikut.

Contoh

Pertimbangkan matriksnya

A={\begin{bmatrix}1&2&3&4\\5&6&7&8\\9&10&11&12\\13&14&15&16\end{bmatrix}}.

A = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{bmatrix}.

Penentu matriks ini dapat dihitung dengan menggunakan ekspansi kofaktor Laplace di sepanjang dua baris pertama sebagai berikut. Pertama-tama perhatikan bahwa ada 6 set dua angka berbeda dalam

{1, 2, 3, 4},

yaitu let

S=\left\{\{1,2\},\{1,3\},\{1,4\},\{2,3\},\{2,4\},\{3,4\}\right\}

S=\left\{\{1,2\},\{1,3\},\{1,4\},\{2,3\},\{2,4\},\{3,4\}\right\}

Dengan mendefinisikan kofaktor komplementer menjadi

b_{\{j,k\}}={\begin{vmatrix}a_{1j}&a_{1k}\\a_{2j}&a_{2k}\end{vmatrix}},

b_{\{j,k\}}={\begin{vmatrix}a_{1j}&a_{1k}\\a_{2j}&a_{2k}\end{vmatrix}},

c_{\{p,q\}}={\begin{vmatrix}a_{3p}&a_{3q}\\a_{4p}&a_{4q}\end{vmatrix}},

c_{\{p,q\}}={\begin{vmatrix}a_{3p}&a_{3q}\\a_{4p}&a_{4q}\end{vmatrix}},

dan tanda permutasi mereka menjadi

\varepsilon ^{\{i,j\},\{p,q\}}={\mbox{sgn}}{\begin{bmatrix}1&2&3&4\\i&j&p&q\end{bmatrix}},{\text{ where }}p\neq i,q\neq j.

\varepsilon ^{\{i,j\},\{p,q\}}={\mbox{sgn}}{\begin{bmatrix}1&2&3&4\\i&j&p&q\end{bmatrix}},{\text{ where }}p\neq i,q\neq j.

Penentu A dapat ditulis sebagai

|A|=\sum _{H\in S}\varepsilon ^{H,H^{\prime }}b_{H}c_{H^{\prime }},

|A| = \sum_{H \in S} \varepsilon^{H,H^\prime}b_{H}c_{H^\prime},

dimana

H^{\prime }

II. INVERS

Invers matriks bisa didefinisikan dimana jika A merupakan suatu matriks kuadrat, maka anda bisa mencari matriks B dengan AB = BA = I. A dikatakan bisa dibalik (invertible) dan B disebut dengan invers dari A. Setelah anda mengetahui pengertiannya, maka selanjutnya anda harus mengerti bagaimana cara memecahkan soal terkait invers matriks.

Rumus

Keterangan :

A-1 : Invers Matriks (A)

Det (A) : Determinan Matriks (A)

Adj (A) : Adjoin Matriks (A)

dewipmeilinda

Saturday, 14 December 2019

MATRIKS DETERMINAN (lanjutan) & INVERS

I. DETERMINAN

a. Metode Sarrus

Tahapan Metode Sarrus dalam Mencari Determinan

B. Metode Minor & Kofaktor

- Minor

Bukti

Laplace ekspansi determinan dengan anak di bawah umur yang saling melengkapi

Contoh

No comments:

Post a Comment

Tugas Kewirausahaan

Report Abuse