INTEGRAL
Integral adalah bentuk operasi matematika yang menjadi invers (kebalikan) dari sebuah operasi turunan dan limit dari jumlah atau suatu luas daerah tertentu.
2. Rule 2 (The Integral Of Multiple)
3. Rule 3 (The Subtitution Rule)
4. Rule 4 (The Logarithmic Rule)
5. Rule 5 (The Exponential Rule)
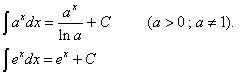
6. Rule 6 (The Integral Of Sum)
7. Rule 7 (Integration by Parts)
Jika u = u(x) dan du = u′(x) dx, sedangkan v = v(x) dan dv = v′(x) dx, lalu integration by parts dinyatakan dengan :
![{\displaystyle {\begin{aligned}\int _{a}^{b}u(x)v'(x)\,dx&=[u(x)v(x)]_{a}^{b}-\int _{a}^{b}u'(x)v(x)dx\\&=u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88aa4b830425c067064d8b5f397f6ea52ed51ada)
atau lebih jelasnya :
8. Rule 8 (Trigonometric Rules)
Integral sebagai invers/kebalikan dari turunan disebut sebagai itegral tak tentu.
· Integral sebagai limit dari jumlah atau suatu luas daerah tertentudisebut integral tentu.
Rumus
integral f(x)dx
· f(x) = fungsi yang akan diintegralkan
· dx = tanda untuk melakukan diferensiasi terhadap x
· integral f(x)dx sebagai notasi diferensiasi dari the primitive function/dari fungsi asalnya.
Rumus dasar integral:
Aturan-Aturan Dasar Integral
1. Rule 1 (The Power Rule)
2. Rule 2 (The Integral Of Multiple)
3. Rule 3 (The Subtitution Rule)
4. Rule 4 (The Logarithmic Rule)
5. Rule 5 (The Exponential Rule)
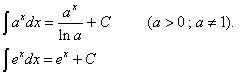
6. Rule 6 (The Integral Of Sum)
7. Rule 7 (Integration by Parts)
Jika u = u(x) dan du = u′(x) dx, sedangkan v = v(x) dan dv = v′(x) dx, lalu integration by parts dinyatakan dengan :
atau lebih jelasnya :
8. Rule 8 (Trigonometric Rules)
No comments:
Post a Comment