Matriks
Definisi Matriks
Matriks adalah susunan sekelompok bilangan dalam suatu jajaran berbentuk persegi panjang yang diatur berdasarkan baris dan kolom dan diletakkan antara dua tanda kurung. Tanda kurung yang digunakan untuk mengapit susunan anggota matriks tersebut dapat berupa tanda kurung biasa atau tanda kurung siku. Setiap bilangan pada matriks disebut elemen (unsur) matriks. Kumpulan elemen yang tersusun secara horizontal disebut baris, sedangkan kumpulan elemen yang tersusun secara vertikal disebut kolom.
Bentuk Matriks

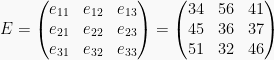
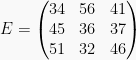





Operasi Perkalian Dua Matriks




Bentuk Matriks
Ordo Matriks
Dijelaskan sebelumnya matriks terdiri dari unsur-unsur yang tersusun secara baris dan kolom. Jika banyak baris suatu matriks adalah m, dan banyak kolom suatu matriks adalah n, maka matriks tersebut memiliki ordo matriks atau ukuran m x n. Perlu diingat bahwa m dan n hanya sebuah notasi, sehingga tidak boleh dilakukan sebuah perhitungan (penjumlahan, perkalian). Pada contoh matriks jumlah penjualan mobil diatas diketahui bahwa:

- Banyak baris, m = 3
- Banyak kolom, n = 3
- Ordo matriks, m x n = 3 x 3
Penamaan/notasi matriks menggunakan huruf kapital, sedangkan elemen-elemen di dalamnya dinotasikan dengan huruf kecil sesuai dengan penamaan matriks dan diberi indeks ij. Indeks tersebut menyatakan posisi elemen matriks, yaitu pada baris i dan kolom j. Sebagai contoh, matriks sebelumnya untuk penjualan mobil:
Dimana,  adalah elemen matriks yang berada pada baris ke-1 (i = 1) dan kolom ke-2 (j = 2). Begitu juga dengan elemen matriks yang lainnya.
adalah elemen matriks yang berada pada baris ke-1 (i = 1) dan kolom ke-2 (j = 2). Begitu juga dengan elemen matriks yang lainnya.
Pada matriks terdapat dua jenis diagonal, yaitu diagonal utama dan diagonal sekunder. Diagonal utama merupakan elemen-elemen dengan yang bisa membentuk garis miring. Diagonal sekunder merupakan kebalikan dari garis miring diagonal utama. Perhatikan matriks berikut:
Diagonal utama adalah elemen 34, 36, 46, sedangkan diagonal sekunder adalah elemen 41, 36, 51.
Penjumlahan Matriks
Operasi hitung matriks pada penjumlahan memiliki syarat yang harus dipenuhi agar dua buah matriks dapay dijumlahkan. Syarat dari dua buah matriks atau lebih dapat dijumlahkan jika memiliki nilai ordo yang sama. Artinya, semua matriks yang dijumlahkan harus memiliki jumlah baris dan kolom yang sama.
Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks dengan jumlah baris 3 dan kolom 4. Matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks dengan jumlah baris 4 dan kolom 3. Kesimpulannya, jumlah baris dan kolom antar dua matriks yang akan dijumlahkan harus sama.
Operasi hitung penjumlahan matriks memenuhi sifat komutatif, asosiatif, memiliki matriks identitas matriks nol, dan memiliki lawan matriks. Lawan matriks A adalah matriks 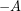 , di mana elemen-elemen matriks
, di mana elemen-elemen matriks 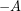 merupakan lawan dari elemen-elemen matriks A. Secara ringkas, sifat operasi penjumlahan matriks dapat dilihat pada gambar di bawah.
merupakan lawan dari elemen-elemen matriks A. Secara ringkas, sifat operasi penjumlahan matriks dapat dilihat pada gambar di bawah.

Selanjutnya, kita akan mempelajari cara melakukan operasi hitung penjumlahan dua buah matriks. Penjelasan akan diberikan dalam bentuk contoh soal secara umum.
Contoh cara melakukan operasi penjumlahan pada matriks:
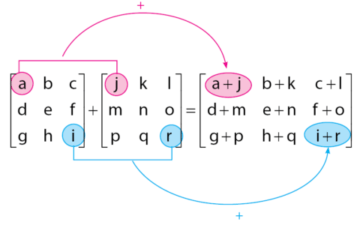
Pengurangan Matriks
Seperti halnya operasi hitung penjumlahan matriks, syarat agar dapat mengurangkan elemen-elemen antar matriks adalah matriks harus memiliki nilai ordo yang sama. Cara melakukan operasi pengurangan pada matriks dapat dilihat seperti cara di bawah.
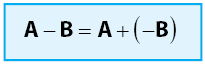
Cara melakukan operasi pengurangan dua matriks tidak jauh berbeda dengan penjumlahan matriks. Untuk lebih jelasnya, perhatikan contoh soal pengurangan matriks secara umum yang akan diberikan di bawah.
Contoh cara melakukan operasi pengurangan pada matriks:
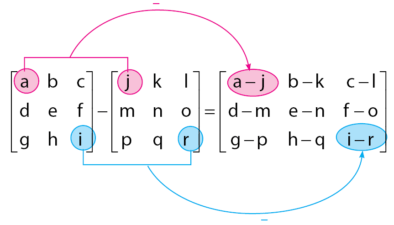
Perkalian Matriks
Pembahasan operasi hitung matriks selanjutnya yang akan dibahas adalah perkalian matriks. Perkalian matriks yang akan dibahas di bawah adalah perkalian matriks dengan skalar dan perkalian matriks dengan matriks. Selengkapnya simak operasi hitung perkalian matriks di bawah.
Perkalian Matriks dengan Skalar
Cara melakukan operasi skalar pada matriks adalah dengan mengalikan semua elemen-elemen matriks dengan skalarnya. Jika k adalah suatu konstanta dan A adalah matriks, maka cara melakukan operasi perkalian skalar dapat dilihat melalui cara di bawah.
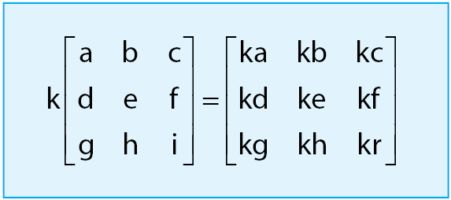
Cara melakukan perkalian matriks dengan skalar cukup mudah dilakukan. Contoh soal cara melakukan perkalian matriks yang akan diberikan di bawah akan menambah pemahaman sobat idschool.
Contoh cara melakukan operasi perkalian skalar pada matriks:
Diketahui konstanta k = 2 dan sebuah matriks A dengan persamaan seperti di bawah.
Maka hasil perkalian konstanta k dengan matriks A adalah sebagai berikut.
Uraian selanjutnya adalah cara melakukan perkalian dua matriks.
Operasi Perkalian Dua Matriks
Seperti yang telah disinggung sebelumnya, syarat dua buah matriks dapat dikalikan jika memiliki jumlah kolom matriks pertama yang sama dengan jumlah baris matriks ke dua. Ordo matriks hasil perkalian dua matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.
Matriks A memiliki jumlah kolom sebanyak m dan jumlah baris r, matriks B memiliki jumlah kolom sebanyak r dan jumlah baris m, hasil perkalian matriks A dan B adalah matriks C dengan jumlah kolom m dan jumlah baris n.
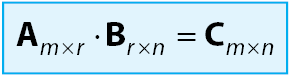
Sebelum mengulas cara melakukan operasi perkalian dua buah matriks, sebaiknya kita perlajari dahulu sidat-sifat operasi perkalian dua matriks. Sifat-sifat operasi perkalian matriks meliputi sifat asosiatif, distributif, dan memiliki matriks identitas I. Sifat-sifat operasi perkalian matriks dapat dilihat pada gambar di bawah.

Sifat-sifat matriks di atas dapat digunakan untuk memudahkan perhitungan dalam melakukan operasi hitung matriks.
Sekarang, pembahasan kita masuk pada perkalian dua matriks. Untuk pembahasan pertama kita akan mempelajari cara melakukan perkalian matriks dengan ukuran 2x2 dan matriks dengan ukuran 2x1
Proses cara melakukan operasi perkalian matriksdengan ukuran 2  2 dan matriks dengan ukuran 2
2 dan matriks dengan ukuran 2  1 dapat disimak pada pembahasan di bawah.
1 dapat disimak pada pembahasan di bawah.
Diketahui:
Perkalian dua matriks AxB dapat diperoleh dengan cara di bawah.
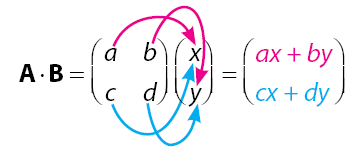
Selanjutnya adalah perkalian dua matriks. Kedua matriks yang akan dioperasikan sama-sama berukuran 2 x 2. Selengkapnya, simak pembahasan di bawah.
Diketahui:
Maka perkalian dua matriks PxQ dapat diperoleh dengan cara di bawah.
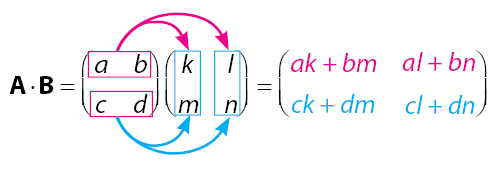
Untuk lebih jelasnya akan ditunjukkan dari contoh soal operasi perkalian dua matriks seperti yang ditunjukkan di bawah.
Diketahui:
Maka:
Transpose Matriks
jenis-jenis Matriks
Misalkan diberikan matriks sebagai berikut:

![Rendered by QuickLaTeX.com \[ \textrm{A} \; = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ 7 & 8 \end{bmatrix}\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-503b41011c0fecdf9e590e018e9aca91_l3.png)
![Rendered by QuickLaTeX.com \[ k\textrm{A} \; = 2 \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ 7 & 8 \end{bmatrix}\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c6b72ab234ed577aa25c0d25e90982d2_l3.png)
![Rendered by QuickLaTeX.com \[ k\textrm{A} \; = \begin{bmatrix} 2 & 4 \\ 6 & 8 \\ 10 & 12 \\ 14 & 16 \end{bmatrix}\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-5d44d7736da3699d6a20ae4e0d75e894_l3.png)
![Rendered by QuickLaTeX.com \[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-99b562685a33f4bf81a506a862328328_l3.png)










No comments:
Post a Comment