GARIS SINGGUNG dan OPTIMASI pada TURUNAN
Garis Singgung
Pengertian Garis Singgung
Dalam ilmu geometri, garis singgung atau biasa disebut juga garis tangen kurva bidang pada titik yang diketahui ialah garis lurus yang “hanya menyentuh” kurva pada titik tersebut.
Leibniz mendefinisikan bahwa suatu garis singgung sebagai garis yang melalui sepasang titik tak hingga dekat pada kurva. Lebih tepatnya, garis lurus ini disebut juga menyinggung kurva y = f (x) di titik x = c pada kurva apabila garis melalui titik (c, f (c)) pada kurva dan memiliki kemiringan f ‘(c) dengan f ‘ ialah turunan f.
Definisi yang serupa juga digunakan pada kurva ruang dan kurva dalam ruang Euklides dimensi –n.
Karena melalui titik di mana garis singgung dan kurva bertemu, maka disebut titik singgung, garis singgung “memiliki arah yang sama” dengan kurva, dan dengan demikian merupakan pendekatan garis lurus terbaik pada kurva pada titik tersebut.
Serupa dengan garis singgung, bidang singgung permukaan pada titik yang diketahui adalah bidang yang “hanya menyentuh” permukaan di titik tersebut. Konsep persinggungan ialah satu dari gagasan paling mendasar dalam geometri diferensial dan telah digeneralisasikan secara ekstensif.
Garis Singgung Persekutuan Luar Dua Lingkaran
Persamaan garis singgung lingkaran persekutuan luar yaitu melibatkan dua lingkaran dan sebuah garis singgung lingkaran. Untuk lebih jelasnya dapat kita lihat pada gambar di bawah berikut:
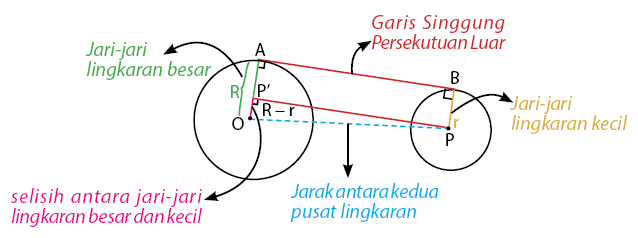
Rumus Mencari Panjang Garis Singgung Persekutuan Luar Dua Lingkaran
Rumus – rumusnya yaitu:
![\[ AB = PP' = \sqrt{OP^{2}-(R-r)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-e3287382bcab3661c25486ef3a1e5cea_l3.svg "Rendered by QuickLaTeX.com")
Keterangannya:
AB = PP’ adalah Garis singgung persekutuan luar lingkaran
OP adalah Jarak antara kedua pusat lingkaran
R adalah Jari-jari lingkaran besar
r adalah Jari-jari lingkaran kecil
AB = PP’ adalah Garis singgung persekutuan luar lingkaran
OP adalah Jarak antara kedua pusat lingkaran
R adalah Jari-jari lingkaran besar
r adalah Jari-jari lingkaran kecil
Garis Singgung Persekutuan Dalam Dua Lingkaran
Seperti pada garis singgung persekutuan luar dua lingkaran, garis singgung persekutuan dalam dua lingkaran ini juga melibatkan antara dua buah lingkaran dan sebuah garis singgung. Bedanya yaitu terletak pada posisi garis singgung lingkaran.
Dua titik singgung lingkaran pada garis singgung persekutuan luar dua lingkaran terletak pada sisi yang sama. Sedangkan dua titik singgung lingkaran pada garis singggung persekutuan dalam dua lingkaran terletak yang bersebrangan. Untuk lebih jelasnya, mari perhatikan gambar dibawah berikut:
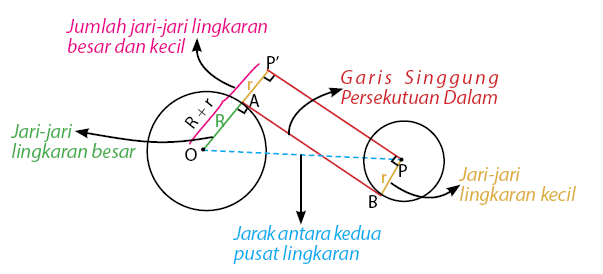
Rumus Mencari Panjang Garis Singgung Persekutuan Dalam
Rumusnya yaitu:
![\[ AB = PP' = \sqrt{OP^{2} - (R + r)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d9bbc516875d78adeb05d4951a45b58f_l3.svg "Rendered by QuickLaTeX.com")
Keterangannya:
AB = PP’ adalah Garis singgung persekutuan luar lingkaran
OP adalah Jarak antara kedua pusat lingkaran
R adalah Jari-jari lingkaran besar
r adalah Jari-jari lingkaran kecil
Contoh Soal dan Cara Menentukannya
Perhatikan gambar berikut ini:
Panjang jari-jari lingkaran besar dan kecil berturut-turut ialah 10 cm dan 5 cm. Jarak kedua pusat lingkaran tersebut adalah 25 cm. Tentukan panjang garis singgung AB adalah ….
Optimasi
Pengertian
Optimasi (Optimization) adalah aktivitas untuk mendapatkan hasil terbaik di bawah keadaan yang diberikan. Tujuan akhir dari semua aktivitas tersebut adalah meminimumkan usaha (effort) atau memaksimumkan manfaat (benefit) yang diinginkan. Karena usaha yang diperlukan atau manfaat yang diinginkan dapat dinyatakan sebagai fungsi dari variabel keputusan, maka optimasi dapat didefinisikan sebagai proses untuk menemukan kondisi yang memberikan nilai minimum atau maksimum dari sebuah fungsi. Optimasi dapat diartikan sebagai aktivitas untuk mendapatkan nilai minimum suatu fungsi karena untuk mendapatkan nilai maksimum suatu fungsi dapat dilakukan dengan mencari minimum dari negatif fungsi yang sama.
Tidak ada metode tunggal yang dapat dipakai untuk menyelesaikan semua masalah optimasi. Banyak metode optimasi telah dikembangkan untuk menyelesaikan tipe optimasi yang berbeda-beda seperti metode Lagrange.
Dalam optimasi diselidiki masalah penentuan suatu titik minimum suatu fungsi pada subset ruang bilangan riil tak kosong. Untuk lebih spesifik dirumuskan sebagai berikut: Misalkan πΉ ruang bilangan riil dan π subset tak kosong dari πΉ, dan misalkan π: π → πΉ sebuah fungsi yang diberikan. Kita akan mencari titik minimum π pada π. Sebuah elemen π₯̅ ∈ π dikatakan titik minimum π pada π jika
π(π₯̅) ≤ π(π₯) untuk semua π₯ ∈ π
Himpunan π dinamakan himpunan pembatas (constraint set) dan fungsi π dinamakan fungsi objektif.
Tidak ada metode tunggal yang dapat dipakai untuk menyelesaikan semua masalah optimasi. Banyak metode optimasi telah dikembangkan untuk menyelesaikan tipe optimasi yang berbeda-beda seperti metode Lagrange.
Dalam optimasi diselidiki masalah penentuan suatu titik minimum suatu fungsi pada subset ruang bilangan riil tak kosong. Untuk lebih spesifik dirumuskan sebagai berikut: Misalkan πΉ ruang bilangan riil dan π subset tak kosong dari πΉ, dan misalkan π: π → πΉ sebuah fungsi yang diberikan. Kita akan mencari titik minimum π pada π. Sebuah elemen π₯̅ ∈ π dikatakan titik minimum π pada π jika
π(π₯̅) ≤ π(π₯) untuk semua π₯ ∈ π
Himpunan π dinamakan himpunan pembatas (constraint set) dan fungsi π dinamakan fungsi objektif.
Metode pencari titik optimum juga dikenal sebagai teknik pemrograman matematikal dan menjadi bagian dari penelitian operasional (operations research). Penelitian operasional adalah suatu cabang matematika yang menekankan kepada aplikasi teknik dan metode saintifik untuk masalah-masalah pengambilan keputusan dan pencarian solusi terbaik atau optimal. Teknik pemrograman matematikal sangat berguna dalam pencarian minimum suatu fungsi beberapa variabel di bawa kendala yang ada. Teknik proses stokastik dapat digunakan untuk menganalisis masalah yang didiskripsikan dengan sekumpulan variabel acak dimana distribusi probabilitasnya diketahui. Metode statistikal dapat digunakan untuk menganalisis data eksperimen dan untuk membangun model secara empirik untuk memperoleh representasi yang lebih akurat mengenai situasi fiskal.
Optimasi Tanpa Kendala
Masalah optimasi yang tidak melibatkan sebarang kendala dinamakan optimasi tanpa kendala dan dinyatakan sebagai:
Minimumkan π = π(π)
π = (π₯1,π₯2,...,π₯π)π
Optimasi Dengan Kendala
Masalah optimasi yang melibatkan sebarang kendala dinamakan optimasi terkendala dan dinyatakan sebagai:
Masalah optimasi yang tidak melibatkan sebarang kendala dinamakan optimasi tanpa kendala dan dinyatakan sebagai:
Minimumkan π = π(π)
π = (π₯1,π₯2,...,π₯π)π
Optimasi Dengan Kendala
Masalah optimasi yang melibatkan sebarang kendala dinamakan optimasi terkendala dan dinyatakan sebagai:
Minimumkan π = π(π)
π = (π₯1,π₯2,...,π₯π)π
dengan kendala:
ππ(π) ≤ 0 π = 1,2,...,π
π (π) = 0 π = 1,2, ... , π π
π = (π₯1,π₯2,...,π₯π)π
dengan kendala:
ππ(π) ≤ 0 π = 1,2,...,π
π (π) = 0 π = 1,2, ... , π π
dimana π adalah sebuah vektor berdimensi- π yang dinamakan vektor disain atau variabel keputusan, π(π) disebut fungsi obyektif, π (π) dan π (π) dikenal sebagai
kendala ketaksamaan dan kendala kesamaan.
kendala ketaksamaan dan kendala kesamaan.
Teknik Optimasi
Metode klasik kalkulus diferensial dapat digunakan untuk mendapatkan maksima dan minima suatu fungsi multi variabel tanpa kendala. Metode ini mengasumsikan bahwa fungsi tersebut dapat didiferensialkan dua kali terhadap variabel keputusan dan turunannya kontinu. Untuk masalah optimasi dengan kendala kesamaan, metode pengali Lagrange (Lagrangian multiplier method) dapat digunakan. Jika masalah optimasi melibatkan kendala kesamaan, syarat Kuhn-Tucker dapat digunakan untuk mengidentifikan titik optimum. Akan tetapi metode ini melibatkan
sekumpulan persamaan non linier secara simultan yang boleh jadi sukar untuk diselesaikan.
Penerapan perhitungan penurunan parsial penting sekali dalam bidang ekonomi, terutama di dalam menentukan nilai optimum suatu fungsi multivariat. Nilai optimum yang dimaksud ialah nilai yang diperoleh dari proses penentuan pemecahan yang paling terbaik dari pemecahan-pemecahan dalam suatu kendala yang ada. Nilai yang diperoleh ini bias maksimum atau minimum.
Penerapan perhitungan penurunan parsial penting sekali dalam bidang ekonomi, terutama di dalam menentukan nilai optimum suatu fungsi multivariat. Nilai optimum yang dimaksud ialah nilai yang diperoleh dari proses penentuan pemecahan yang paling terbaik dari pemecahan-pemecahan dalam suatu kendala yang ada. Nilai yang diperoleh ini bias maksimum atau minimum.
Maksimum Dan Minimum
Teorema keberadaan Maksimum-Minimum
Nilai ektrem suatu fungsi bisa nilai maksimum atau nilai minimum. Disini dibedakan antara nilai maksimum global atau absolut dengan maksimum lokal atau relatif dan nilai minimum global atau absolut dengan maksimum lokal atau relatif.
Dari gambar diketahui bahwa titik B adalah titik maksimum global sedangkan titik E adalah titik maksimum lokal. Titik D adalah minimum global sedangkan titik F adalah titik minimum lokal. Titik C bukanlah titik maksimum atau minimum suatu fungsi, titik ini disebut titik belok suatu fungsi.
Titik maksimum terjadi jika koefisien arah dari garis singgung pada garis tersebut adalah nol dan kurva terbuka kebawah, sedangkan titik minimum terjadi jika koefisien arah dari garis singgung pada titik tersebut adalah nol dan kurva terbuka ke atas.
Dari gambar diketahui bahwa titik B adalah titik maksimum global sedangkan titik E adalah titik maksimum lokal. Titik D adalah minimum global sedangkan titik F adalah titik minimum lokal. Titik C bukanlah titik maksimum atau minimum suatu fungsi, titik ini disebut titik belok suatu fungsi.
Titik maksimum terjadi jika koefisien arah dari garis singgung pada garis tersebut adalah nol dan kurva terbuka kebawah, sedangkan titik minimum terjadi jika koefisien arah dari garis singgung pada titik tersebut adalah nol dan kurva terbuka ke atas.
Jika π kontinu pada sebuah himpunan π tertutup terbatas, maka π mencapai nilai maksimum (global) dan nilai minimum (global) di himpunan tersebut.
Misalkan π adalah fungsi dengan daerah asal π, dan misalkan π0 adalah sebuah titik di π.
Masalah mencari nilai maksimum atau minimum akan sangat sulit jika bentuk umum daripada kurva belum diketahui. Di dalam hal ini sangatlah sukar menentukan apakah titik kritisnya adalah titik maksimum, titik minimum, atau titik lainnya. Cara yang paling mudah ialah dengan mencari turunan pertama atau turunan kedua yang dekat nilai kritisnya.
Misalkan π adalah fungsi dengan daerah asal π, dan misalkan π0 adalah sebuah titik di π.
- π(π0) adalah nilai maksimum global dari π di π jika π(π0) ≥ π(π) untuk seluruh π di π.
- π(π0) adalah nilai minimum global dari π di π jika π(π0) ≤ π(π) untuk seluruh π di π.
- π(π0) adalah nilai ekstrem global dari π di π jika π(π0) bukan nilai maksimum global dan bukan nilai minimum global.
Untuk menentukan nilai ekstrem fungsi adalah dengan menentukan titik di
Masalah mencari nilai maksimum atau minimum akan sangat sulit jika bentuk umum daripada kurva belum diketahui. Di dalam hal ini sangatlah sukar menentukan apakah titik kritisnya adalah titik maksimum, titik minimum, atau titik lainnya. Cara yang paling mudah ialah dengan mencari turunan pertama atau turunan kedua yang dekat nilai kritisnya.
No comments:
Post a Comment