BARIS DAN DERET DALAM MATEMATIKA

Baris 

Barisan dalam matematika, adalah suatu daftar tertata. Sebagaimana suatu himpunan, urutan memuat "anggota" atau "elemen" (juga disebut "suku" atau "istilah"). Jumlah elemen tertata (kemungkinan tak terhingga) disebut panjang urutan. Berbeda dengan himpunan, penataan urutan sangat penting dan elemen-elemen yang tepat sama dapat muncul berulang kali pada posisi berbeda dalam urutan itu. Lebih tepatnya, suatu urutan dapat didefinisikan sebagai suatu fungsi di mana ranah (atau domain) darinya merupakan suatu himpunan countable totally ordered, sepertu bilangan asli.

Baris Aritmatika

Baris aritmatika merupakan baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui penjumlahan atau pengurangan dengan suatu bilangan b. Selisih antara nilai suku-suku yang berdekatan selalu sama yaitu b. Sehingga:

Sebagai contoh baris 1, 3, 5, 7, 9, merupakan baris aritmatika dengan nilai:

b = (9 – 7) = (7 – 5) = (5 – 3) = (3 – 1) = 2

Untuk mengetahui nilai suku ke-n dari suatu barisan aritmatika dapat diketahui dengan mengetahui nilai suku ke-k dan selisih antar suku yang berdekatan (b). rumusannya berikut ini:

Jika yang diketahui adalah nilai suku pertama 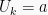 dan selisih antar sukunya (b), maka nilai k = 1 dan nilai  adalah:

Barisan Geometri

Baris geometri adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan r. Perbandinganatau rasio antara nilai suku dengan nilai suku sebelumnya yang berdekatan selalu sama yaitu r. Sehingga:

Sebagai contoh baris 1, 2, 4, 8, 16, merupakan baris geometri dengan nilai

Untuk mengetahui nilai suku ke-n dari suatu barisan geometri dapat diketahui dengan mengetahui nilai suku ke-k dan rasio antar suku yang berdekatan (r). Rumusannya berikut ini:

Jika yang diketahui adalah nilai suku pertama 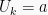  dan rasio antar sukunya (r), maka nilai k = 1 dan nilai  adalah:

Deret

Deret adalah jumlah dari elemen-elemen  dalam suatu urutan. Urutan dan deret finit (atau terhingga) mempunyai elemen pertama dan terakhir yang terdefinisi, sedangkan Urutan dan deret infinit (atau tak terhingga) berlangsung terus menerus tak terbatas.^[1]

Dalam matematika, jika ada suatu urutan bilangan infinite { a_n }, maka suatu deret secara informal adalah hasil dari penambahan semua elemen-elemen itu bersama-sama: a₁ + a₂ + a₃ + · · ·. Ini dapat ditulis lebih singkat menggunakan simbol summation ∑. 

Deret Aritmatika

Deret aritmatika adalah penjumlahan suku-suku dari suatu barisan aritmatika. Penjumlahan dari suku-suku petama sampai suku ke-n barisan aritmatika dapat dihitung sebagai:

atau sebagai:

Jika hanya diketahui nilai a dalalah suku pertama dan nilai adalah suku ke-n, maka nilai deret aritmatikanya adalah:

Persamaan tersebut bisa dibalik untuk mencari nilai suku ke-n menjadi:

.

.

Sehingga diperoleh .

Deret Geometri

Deret geometri adalah penjumlahan suku-suku dari suatu barisan geometri. Penjumlahan dari suku suku petama sampai suku ke-n barisan geometri dapat dihitung sebagai:

Deret Geometri Tak hingga

Suatu deret geometri dapat menjumlakan suku-sukunya sampai menuju tak hingga. Apabila deret geometri menuju tak hingga dimana , maka deret ini dapat dijumlah menjadi:

Atau sebagai :

Deret geometri tak hingga terdiri dari 2 jenis yaitu konvergen dan divergen. Deret geometri tak hingga bersifat konvergen jika penjumlahan dari suku-sukunya menuju atau mendekati suatu bilangaan tertentu. Sedangkan bersifat divergen jika penjumlahan dari suku-sukunya tidak terbatas. Nilai deret geometri tak hingga dapat diperoleh dengan mengunakan limit. Sebelumnya diketahui bahwa nilai deret geometri  adalah:

Dimana terdapat unsur 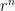 didalam perhitungannya yang terpengaruh jumlah suku n. Jika , maka untuk menentukan nilai 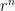 dapat menggunakan limit yaitu:

dengan syarat -1 < r < 1.

Dan:

dengan syarat r < -1 atau r > 1.

Kemudian hasil limit 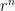 tersebut dapat dimasukan kedalam perhitungan deret sebagai:

dengan syarat -1 < r < 1

Dan:

HUUBUNGAN DAN FUNGSI DALAM MATEMATIKA

HUBUNGAN (Relasi)

Relasi yaitu hubungan antara anggota pada suatu himpunan dengan anggota himpunan yang lainya. Relasi dari himpunan A ke himpunan B ialah menghubungkan anggota-anggota himpunan A pada anggota-anggota himpunan B.

Cara Menyatakan Relasi: 

1. Diagram Panah

Diagram panah itu merupakan sebuah diagram yang digunakan untuk menunjukkan hubungan antara himpunan awal ( domain ) dengan himpunan tujuan ( codomain ) yang diumpamakan dengan tanda panah.

   

2. Diagram Cartesius

Diagram Cartesius merupakan diagram yang terdiri dari sumbu X dan sumbu Y. Pada diagram kartesius, anggota himpunan P terletak pada sumbu x, sedangkan anggota himpunan Q terletak pada sumbu y Relasi yang menghubungkan himpunan P dan Q ditunjukkan dengan noktah ataupun titik.

3. Himpunan Pasangan Berurutan

Sebuah relasi yang menghubungkan himpunan yang satu dengan himpunan lainnya bisa disajikan pada bentuk himpunan pasangan berurutan. Cara penulisannya yaitu anggota himpunan P ditulis pertama, sedangkan anggota himpunan Q menjadi pasangannya.

Contoh :

{(Rani, basket)}, {(Rani, bulu tangkis)}, {(Dian, basket)}, {(Dian, atletik)}, {(Isnie, senam)}, {(Dila, basket)}, {(Dila, tenis meja)}

JENIS JENIS RELASI:

1. Relasi Invers

Misalkan R adalah relasi dari himpunan A ke himpunan B. Invers dari R yang dinyatakan dengan relasi dari B ke A yang mengandung semua pasangan terurut yang apabila dipertukarkan masih termasuk dalam R. Ditulis dalam notasi himpunan sebagai berikut ; R-1= {(b,a) : (a,b)R}

Contoh:

A = {1,2,3} B = {x,y}

R = {(1,x), (1,y), (3,x)} relasi dari A ke B
R-1= {(x,1), (y,1), (x,3)} relasi invers dari B ke A

2. Relasi Simetrik

Misalkan R = (A, B, P(x,y)) suatu relasi. R disebut relasi simetrik, jika tiap (a,b)R berlaku (b,a)R. Dengan istilah lain, R disebut juga relasi simetrik jika a R b berakibat b R a.

Contoh Relasi Simetrik :
perhatikan satu per satu. Setiap kali kamu menemukan pasangan, misalnya (a, b), maka cari apakah (b, a) juga ada. Kalau ternyata tidak ada, pasti relasi itu tidak simetrik.

3. Relasi Refleksif

Misalkan R = (A, A, P(x,y)) suatu relasi. R disebut relasi refleksif, jika setiap A berlaku (a,a)R. Dengan kata lain, R disebut relasi refleksif jika tiap-tiap anggota pada A berelasi dengan dirinya sendiri

Contoh :
Relasi Refleksif Diketahui A = {1, 2, 3, 4} dan R = {(1,1), (2,3), (3,3), (4,2), (4,4)} Apakah R relasi refleksif ? R bukan relasi refleksif, karna (2,2) tidak termasuk dalam R. Jika (2,2) termasuk dalam R, yaitu R1= {(1,1), (2,2), (2,3), (3,3), (4,2), (4,4)} maka R1 merupakan relasi refleksif.

4. Relasi anti Simetrik

Suatu relasi R bisa disebut relasi anti simetrik andai (a,b)R dan (b,a)R maka a=b. Dengan kata lain Jika a, b A, a≠b, maka (a,b)R atau (b,a)R, tetapi tidak kedua-duanya.

Contoh :
Misalkan R suatu relasi pada himpunan bilangan asli yang didefinisikan “y habis dibagi oleh x”, maka R merupakan relasi anti simetrik sebab jika b habis dibagi a dan a habis dibagi b, maka a = b.
Misalkan A = {1, 2, 3} dan R1= {(1,1), (2,1), (2,2), (2,3), (3,2)}, maka R1bukan relasi anti simetrik, sebab (2,3)R1dan (3,2)R1.

5. Relasi Transitif

Misalkan R relasi dalam himpunan A. R disebut relasi transitif jika berlaku ; (a,b)R dan (b,c)R maka (a,c)R. Dengan kata lain andai a berelasi dengan b dan b berelasi dengan c, maka a berelasi dengan c.

Contoh :
Misalkan A = {a, b, c} dan R = {(a,b), (a,c), (b,a), (c,b)}, maka R bukan relasi transitif, sebab (b,a)R dan (a,c)R tetapi (b,c)R. dilengkapi agar R menjadi relasi transitif R = {(a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c)}

FUNGSI 

Fungsi dalam matematika adalah suatu relasi yang menghubungkan setiap anggota x dalam suatu himpunan yang disebut daerah asal (Domain) dengan suatu nilai tunggal f(x) dari suatu himpunan kedua yang disebut daerah kawan (Kodomain). Himpunan nilai yang diperoleh dari relasi tersebut disebut daerah hasil ( Range).

Sifat Fungsi dalam Matematika:

1. Fungsi Injektif

Sifat fungsi yang pertama adalah injektif atau juga disebut fungsi satu-satu. Secara harfiah mungkin belum bisa kita pahami secara gamblang. Nah, untuk lebih mudah memahamkan sifat fungsi ini, kami contohkan kepada anda, misal fungsi f menyatakan A ke B maka fungsi f disebut suatu fungsi satu-satu (injektif), apabila setiap dua elemen yang berlainan di A akan dipetakan pada dua elemen yang berbeda di B. Selanjutnya secara singkat dapat dikatakan bahwa f:A→B adalah fungsi injektif apabila a ≠ b berakibat f(a) ≠ f(b) atau ekuivalen, jika f(a) = f(b) maka akibatnya a = b.

2. Fungsi Surjektif

Fungsi f: A → B disebut fungsi kepada atau fungsi surjektif jika dan hanya jika untuk sembarang b dalam kodomain Bterdapat paling tidak satu a dalam domain A sehingga berlaku f(a) = b. Dengan kata lain, suatu kodomain fungsi surjektif sama dengan kisarannya (range).

3. Fungsi Bijektif

Sifat fungsi matematika yang terakhir ada;ah bijektif. Suatu pemetaan f: A→B sedemikian rupa sehingga f merupakan fungsi yang injektif dan surjektif sekaligus, maka dikatakan “f adalah fungsi yang bijektif” atau “ A dan B berada dalam korespondensi satu-satu.

Jenis-jenis Fungsi dalam Matematika

1. Fungsi Linear

Jenis pertama adalah fugsi linear. Fungsi pada bilangan real yang didefinisikan : f(x) = ax + b, a dan b konstan dengan a ≠ 0 disebut fungsi linear.

2. Fungsi Konstan

Untuk lebih memudahkan anda untuk memahami jenis fungsi yang kedua ini, kami berikan contoh. Misal f:A→B adalah fungsi di dalam A maka fungsi f disebut fugsi konstan jika dan hanya jika jangkauan dari f hanya terdiri dari satu anggota.

3. Fungsi Identitas

Jenis fungsi berikutnya adalah fungsi identitas. Contoh: f:A→B adalah fungsi dari A ke B maka f disebut fungsi identitas jika dan hanya jika range f = kodomain atau f(A)=B.

4. Fungsi Kuadrat

Jenis fungsi matematika yang terakhir adalah fungsi kuadrat. Fungsi f: R→R yang ditentukan oleh rumus f(x) = ax2 + bx + c dengan a,b,c ∈ R dan a ≠ 0 disebut fungsi kuadrat.

ELEMEN,  HIMPUNAN, dan BILANGAN  dalam MATEMATIKA 

ELEMEN 

Elemen atau anggota (bahasa Inggris: member) dari suatu himpunan dalam matematika adalah objek-objek matematika tertentu yang membentuk himpunan itu.

 HIMPUNAN

Himpunan adalah (kumpulan objek yang memiliki sifat yg dapat didefinisikan dengan jelas) segala koleksi benda-benda tertentu yang dianggap sebagai satu kesatuan. Walaupun hal ini merupakan ide yang sederhana, tidak salah jika himpunan merupakan salah satu konsep penting dan mendasar dalam matematika modern, dan karenanya, studi mengenai struktur kemungkinan himpunan dan teori himpunan, sangatlah berguna.

Berikut istilah-istilah penting yang ada di Himpunan:

1. Kardinalitas
    Pertama adalah Kardinalitas . Kardinalitas dari sebuah himpunan dapat diartikan sebagai ukuran banyaknya elemen yang dikandung oleh himpunan tersebut.Kardinalitas sendiri memiliki pengertian yaitu himpunan bilangan yang menunjukkan banyaknya Jumlah Anggota. Jumlah unsur dalam suatu himpunan dinamakan kardinalitas dari himpunan tersebut. untuk menyatakan banyaknya anggota yang berbeda dalam suatu himpunan menggunakan notasi n. 
Contohnya adalah tentukan banyaknya anggota himpunan A= { Huruf pembentuk kata “cermat“ } . Berarti kamu menjawabnya dengan cara n(A) = 6.




2. Himpunan Semesta  

Pengertian dan Definisi Himpunan Semesta. Himpunan semesta disebut juga semesta pembicaraan. Himpunan semesta atau semesta pembicaraan adalah himpunan yang memuat semua anggota atau objek himpunan yang dibicarakan. Himpunan semesta (semesta pembicaraan) biasanya dinyatakan dengan notasi S. Cara termudah dalam menyatakan himpunan semesta atau semesta pembicaraan adalah dengan menggunakan diagram Venn. Dengan diagram Venn segala operasi himpunan yang terjadi dalam himpunan semesta dapat digambarkan. Operasi himpunan yang mungkin terjadi dalam sebuah semesta pembicaraan antara lain adalah:

a. Himpunan bagian ( ⊂ )

Himpunan bagian adalah himpunan yang menjadi anggota himpunan lainnya yang masih merupakan bagian dari semesta pembicaraan. Contohnya himpunan bagian adalah: Jika S = {P, A, B}, P = {A, B}, dan B = {A}  atau bisa juga di tuliskan A ⊂ B ⊂ P ⊂ S. Dengan diagram Venn contoh soal di atas dapat digambarkan seperti pada gambar disamping.

b. Irisan Himpunan (  )

Irisan himpunan atau intersection adalah anggota suatu himpunan yang juga menjadi anggota himpunan lain. Contoh irisan himpunan adalah: jika S = {A, B} A = {1, 2, 3, 4, 5} dan B = {2, 4, 6, 8, 10 } atau bisa di tuliskan dengan notasi pembentuk himpunan S = {A, B} dan B  A = {2, 4}. Dengan diagram Venn Irisan himpunan dapat digambarkan seperti pada gambar disamping. Irisan himpunan adalah daerah yang berwarna kelabu.

c. Gabungan Himpunan (   )

Gabungan Himpunan adalah pengabungan dua himpunan yang berbeda karena memiliki anggota yang sama. Contohnya: Jika S = {P, Q}  P = { p, i, s, a, u} Q = { s, i, p, a, u} karena memiliki anggota yang sama maka kedua himpunan tadi dapat dituliskan dengan notasi P   Q, dapat digambarkan dengan diagram venn seperti disamping ini.

3. Himpunan Kosong

Himpunan kosong artinya himpunan yang tidak mempunyai anggota. Himpunan kosong ditulis dengan notasi atau simbol { } atau ∅. Contohnya yaitu jika kamu disuruh untuk menyebutkan nama hari yang berawalan dari huruf z, tetapi tidak ada jawabannya karena tidak ada hari yang berawalan huruf z. Berati itu termasuk himpunan kosong. Dijawab seperti ini yaa: n(E) = { } atau n(E) = ∅. Tapi ingat ya Squad, jangan menuliskan himpunan kosong dengan cara n(E) = {0}. Ini salah ya! Ini karena {0} mempunyai anggota yaitu 0, bukan himpunan kosong.

 BILANGAN

#BILANGAN ASLI

Bilangan asli adalah himpunan bilangan bulat positif yang bukan nol.

Nama lain dari bilangan ini adalah bilangan hitung atau bilangan yang bernilai positif (integer positif).

Contoh :

{1, 2, 3, 4, 5, 6, 7, 8, 9, ...}

#BILANGAN CACAH

Bilangan cacah adalah himpunan bilangan asli ditambah dengan nol.

Contoh :

{0, 1, 2, 3, 4, 5, 6, 7, 8, ...}

#BILANGAN NEGATIF

Bilangan negatif

(integer negatif) adalah bilangan yang lebih kecil/ kurang dari nol. Atau juga bisa dikatakan bilangan yang letaknya disebelah kiri nol pada garis bilangan.

Contoh :

{-1, -2, -3, -4, -5, -6, -7, -8, -9, ...}

#BILANGAN BULAT

Bilangan bulat merupakan bilangan yang terdiri dari bilangan asli, bilangan nol dan bilangan negatif.

Contoh :

{-4, -3, -2, -1, 0, 1, 2, 3, 4, ...}

#BILANGAN PRIMA

Bilangan prima adalah bilangan asli lebih besar dari 1 yang faktor pembaginya adalah 1 dan bilangan itu sendiri.

Contoh :

{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...}

#BILANGAN KOMPOSIT

Bilangan komposit adalah bilangan asli lebih besar dari 1 yang bukan merupakan bilangan prima. Bilangan komposit dapat dinyatakan sebagai faktorisasi bilangan bulat, atau hasil perkalian dua bilangan prima atau lebih. Atau bisa juga disebut bilangan yang mempunyai faktor lebih dari dua.
Contoh :
{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, …}

#BILANGAN KOMPLEKS

Bilangan kompleks adalah

suatu bilangan yang merupakan penjumlahan antara bilangan real dan bilangan imajiner atau bilangan yang berbentuk a + bi. Dimana a dan b adalah bilangan real, dan i adalah bilangan imajiner tertentu. Bilangan real a disebut juga bagian real dari bilangan kompleks, dan bilangan real b disebut bagian imajiner. Jika pada suatu bilangan kompleks, nilai b adalah 0, maka bilangan kompleks tersebut menjadi sama dengan bilangan real a.

Contoh :

{3 + 2i}

#BILANGAN IMAJINER

Bilangan imajiner adalah bilangan yang mempunyai sifat i2 = −1. Bilangan ini merupakan bagian dari bilangan kompleks. Secara definisi, bilangan imajiner i ini diperoleh dari penyelesaian persamaan kuadratik :

   x2 + 1 = 0
atau secara ekuivalen 
   x2 = -1
atau juga sering dituliskan sebagai
   x = √-1

#BILANGAN REAL

Bilangan real atau bilangan riil

menyatakan bilangan yang dapat dituliskan dalam bentuk decimal, seperti 2,86547… atau 3.328184. Dalam notasi penulisan bahasa Indonesia, bilangan desimal adalah bilangan yang memiliki angka di belakang koma “,” sedangkan menurut notasi ilmiah, bilangan desimal adalah bilangan yang memiliki angka di belakang tanda titik “.”. Bilangan real meliputi bilangan rasional, seperti 42 dan −23/129, dan bilangan irrasional, seperti π dan √2, dan dapat direpresentasikan sebagai salah satu titik dalam garis bilangan.

Himpunan semua bilangan riil dalam matematika dilambangkan dengan R (berasal dari kata “real”).

#BILANGAN IRRASIONAL

Bilangan irrasional merupakan bilangan real yang tidak bisa dibagi atau lebih tepatnya hasil baginya tidak pernah berhenti. Sehingga tidak bisa dinyatakan a/b.

Contoh :

π      =          3,141592653358…….. 

√2    =          1,4142135623……..

e      =          2,71828281284590…….

#BILANGAN RASIONAL

Bilangan rasional adalah bilangan-bilangan yang merupakan rasio (pembagian) dari dua angka (integer) atau dapat dinyatakan dengan a/b, dimana a merupakan himpunan bilangan bulat dan b merupakan himpunan bilangan bulat tetapi tidak sama dengan nol. Bilangan  Rasional  diberi lambang Q (berasal dari bahasa Inggris “quotient”).

Contoh :

{½, ⅓, ⅔, ⅛, ⅜, ⅝, ⅞, ...}

Bilangan pecahan termasuk sekumpulan bilangan rasional. Pecahan desimal adalah pecahan-pecahan dengan bilangan penyebut 10, 100, dst. { 1/10, 1/100, 1/1000 }, semua bilangan ini dapat ditemukan dalam garis-garis bilangan.

Sebuah bilangan asli dapat dinyatakan dalam bentuk bilangan rasional. Sebagai contoh bilangan asli  2 dapat dinyatakan sebagai 12/6 atau 30/15 dan sebagainya.

#BILANGAN PECAHAN

Bilangan pecahan adalah bilangan yang disajikan/ ditampilkan dalam bentuk a/b; dimana a, b bilangan bulat dan b ≠ 0.

a disebut pembilang dan b disebut penyebut.

#BILANGAN GENAP
Bilangan Genap adalah bilangan bulat yang habis dibagi dua.
Contoh : Bilangan 2, 4, 6, 8, 10, 14, 20,… dll.

#BILANGAN GANJIL
Bilangan Ganjil adalah bilangan bulat yang tidak habis dibagi dua.
Contoh : Bilangan 1, 3, 5, 7, 11, 17, 21, 31,… dll.